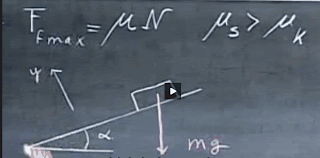
Calculating the Coefficient of Friction using Inclined Plane

Given:

• The normal force is always perpendicular to the plane supporting the mass
• The y axis is perpendicular to the plane supporting the mass
• The x axis is perpendicular to the y axis
• mu is the dimensionless coefficient of friction
• The mu before the object moves is a static mu
• The mu after the object moves is a kinetic mu
• The static mu is always greater than the kinetic mu
• Force due to gravity toward the center of the earth is mg

Definition: General friction forces

• $$ F_{friction} = \mu {F_{normal}} $$
• $$ F_{gravity} = m g $$
• $$ F_{friction} = \mu m g$$

Definition: Forces acting on mass on inclined plane

• $$ \alpha_{angle-of-incline}$$
• $$ F_{normal} = F_y = mg\cos\alpha $$
• $$ F_{down-surface} = F_{friction}$$
• $$ F_{down-surface} = F_x = mg \sin\alpha $$
• $$ F_{friction} = \mu F_y = \mu mg \cos\alpha $$
• $$ mg\sin\alpha = \mu mg \cos\alpha $$
• $$ \mu = \frac{\sin\alpha}{\cos\alpha} $$
• $$ \sin = \frac{opposite}{hypotunese} $$
• $$ \cos = \frac{adjacent}{hypotunese} $$
• $$ \frac{\sin}{\cos} = \frac{\frac{opposite}{hypotunese}}{\frac{adjacent}{hypotunese}} $$
• $$ \frac{\sin}{\cos} = \frac{opposite}{hypotunese} \frac{hypotunese}{adjacent} $$
• $$ \frac{\sin}{\cos} = \frac{opposite}{adjacent} = \tan $$
• $$ \mu = tan\alpha $$
• So we now can use an adjustable inclined plane, raise the angle alpha until the object just breaks loose, measure the angle alpha, and set the static coefficient of friction equal to the tangent of angle alpha. Notice the static mu does not depend on:
• The mass of the object
• The surface area the object is in contact